# Integration by Substitution
Integration by substitution is used to undo [[Derivative Chain Rule]].
Substitution works by rewriting $f(x)$ into $f(u)$. The trick is to introduce a function $u(x)$ in such a way that parts of $du$ also appear in $f(x)$.
For example if determining $\int x\sqrt {1+x^2} \; dx$ define $u$ as $u = 1 + x^2$:
$
\begin{gather}
u = 1+x^2 \\
\frac {du}{dx} = 2x \\
dx = \frac 1 {2x} du \\
\int x\sqrt{1+x^2} \, dx = \int x\sqrt u \frac {1} {2x}du = \int \frac 1 2 \sqrt u \, du
\end{gather}
$
The last expression is much easier to integrate, following the polynomial rule:
![[Antiderivative#^suvvl2]]
$
\int x\sqrt{1+x^2} \, dx = \int \frac 1 2 \sqrt u \, du = \frac 1 2 \frac 2 3 u^{\frac 3 2} = \frac 1 3 \left (1+x^2 \right)^{\frac 3 2}
$
## Using Substitution with Definite Integrals
When applying substitution with definite integrals don't forget to update the bounds! The $du$ integral should be expressed using $u$ bounds, and the initial integral is expressed using $x$ bounds.
For example if tasked to determine $\int \limits_0^\pi \sin(2x) \, dx$ it is useful to define $u = 2x$. $dx = \frac 1 2 du$ and we can write:
$
\int \limits_{x=0}^{x=\pi} \sin(2x)dx = \int \limits_{u=0}^{u=2\pi} \frac 1 2 \sin u \, du
$
The important thing to note above is the change of units, allowing us to skip substituting $u$ at the end of antiderivation.
Because the area under sine from 0 to $2\pi$ is 0 (the period of sine is $2\pi$) the value of the above is 0.
## Trigonometric Substitutions
When dealing with expressions that include $a^2-x^2$, $a^2+x^2$ and $x^2-a^2$ we can use trigonometric substitutions.
| Integrant | Substitution | $\frac {dx} {d\theta}$ | $\theta$ |
| --------- | ------------------------------------------------- | ------------------------- | --------------------- |
| $a^2-x^2$ | $x=a\sin \theta$, $a^2-x^2 = a^2 \cos^2 \theta$ | $a\cos\theta$ | $\arcsin \frac x a$ |
| $a^2+x^2$ | $x=a\tan \theta$, $a^2 + x^2 = a^2 \sec^2 \theta$ | $a\sec^2 \theta$ | $\arctan \frac x a$ |
| $x^2-a^2$ | $x=a\sec\theta$, $x^2 - a^2 = a^2 \tan^2 \theta$ | $a\sec\theta \tan \theta$ | $\sec^{-1} \frac x a$ |
^54k49h
### Reasoning Behind Trigonometric Substitutions
The following triangles describe the substitution for $a=1$:
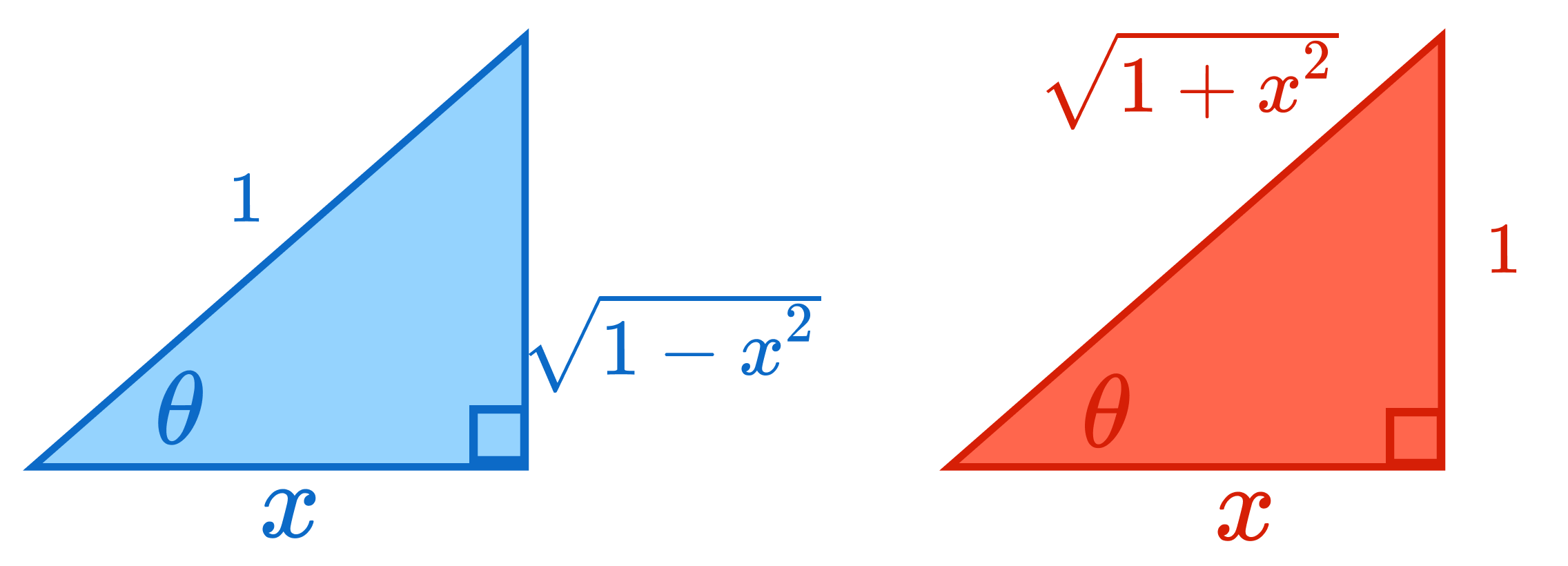
The blue triangle is part of the unit circle whose sides correspond to $(\cos x, \sin x)$. Accordingly we can introduce the following substitution:
$
\begin{gather}
x = \cos \theta \\
\frac {dx}{d\theta} = -\sin \theta
\end{gather}
$
Determining the antiderivative is then significantly simplified. In the end though we'll get a function of $\theta$ so we need to reverse the substitution: $\theta = \arccos x$.
The red triangle is a bit harder to see because the hypothenuse is not constant. Still, we can eliminate it by using $\tan$ or $\cot$. It makes sense to use $\cot$ in this case because the opposite side is 1:
$
\begin{gather}
\cot \theta = \frac {\cos \theta} {\sin \theta} = \frac {\frac x {\sqrt {1+x^2}}} {\frac 1 {\sqrt {1+x^2}}} = x \\
x = \cot \theta \\
\frac {dx} {d\theta} = -\csc^2 \theta
\end{gather}
$
### Trigonometric Substitutions with Definite Integrals
When using trigonometric substitution with definite integrals it is important to be careful with the domain of the inverse functions. Because trigonometric functions are not invertible on their whole domain, inverse functions have limited domain, so you have to use the correct limit substitutions.
For instance take $\int \limits_{x=1}^{x=1} \sqrt {1-x^2}dx$. When applying substitution $x=\cos \theta$, the new limits need to be from $\theta = \pi$, and not from $\theta = -\pi$ to 0, even though $\cos (-\pi$) is also -1. This is because the range of $\arccos$ is always positive.