#readwise # What Does Area Have To Do With Slope?  ## Metadata - Author: [[3Blue1Brown]] - Full Title: What Does Area Have To Do With Slope? - URL: https://www.youtube.com/watch?v=FnJqaIESC2s ## Summary This text explains how to find the average value of a continuous function, specifically using the sine function, by relating it to integration. It demonstrates that the average height of the sine graph can be calculated by dividing the area under the curve by the interval width. The discussion shows how integrals and derivatives are connected, emphasizing that the average value can be interpreted as the slope of the antiderivative. Overall, it highlights the importance of using integrals to generalize concepts of averages to continuous variables. ## Document Notes 1. How does the concept of finding the average height of a sine wave illustrate the relationship between integration and the idea of continuous variables? 2. In what ways does the process of approximating the average height using finite samples help clarify the concept of limits and integrals? 3. Why does the average slope of a graph over an interval correspond to the average value of its derivative, and how does this reinforce the idea that integrals and derivatives are inverses of each other? ## Highlights It's kind of a weird question to think about though, isn't it? The average of a continuous variable. Usually, with averages, we think of a finite number of variables, where you can add them all up and divide that sum by how many there are. But there are infinitely many values of $\sin(x)$ between 0 and $\pi$, and it's not like we can just add up all those numbers and divide by infinity. This sensation comes up a lot in math, and it's worth remembering, where you have this vague sense that you want to add together infinitely many values associated with a continuum, even though that doesn't make sense. And almost always, when you get that sense, the key is to use an integral somehow. And to think through exactly how, a good first step is to just approximate your situation with some kind of finite sum. ([View Highlight](https://read.readwise.io/read/01jfmq0ed3wbnevs7md8q8fg4b)) ^74fiy5 --- For that integral, remember, you also think of a sample of inputs on this continuum, but instead of adding the height $\sin(x)$ at each one and dividing by how many there are, you add up $\sin(x) \times dx$, where $dx$ is the spacing between the samples. That is, you're adding up little areas, not heights. 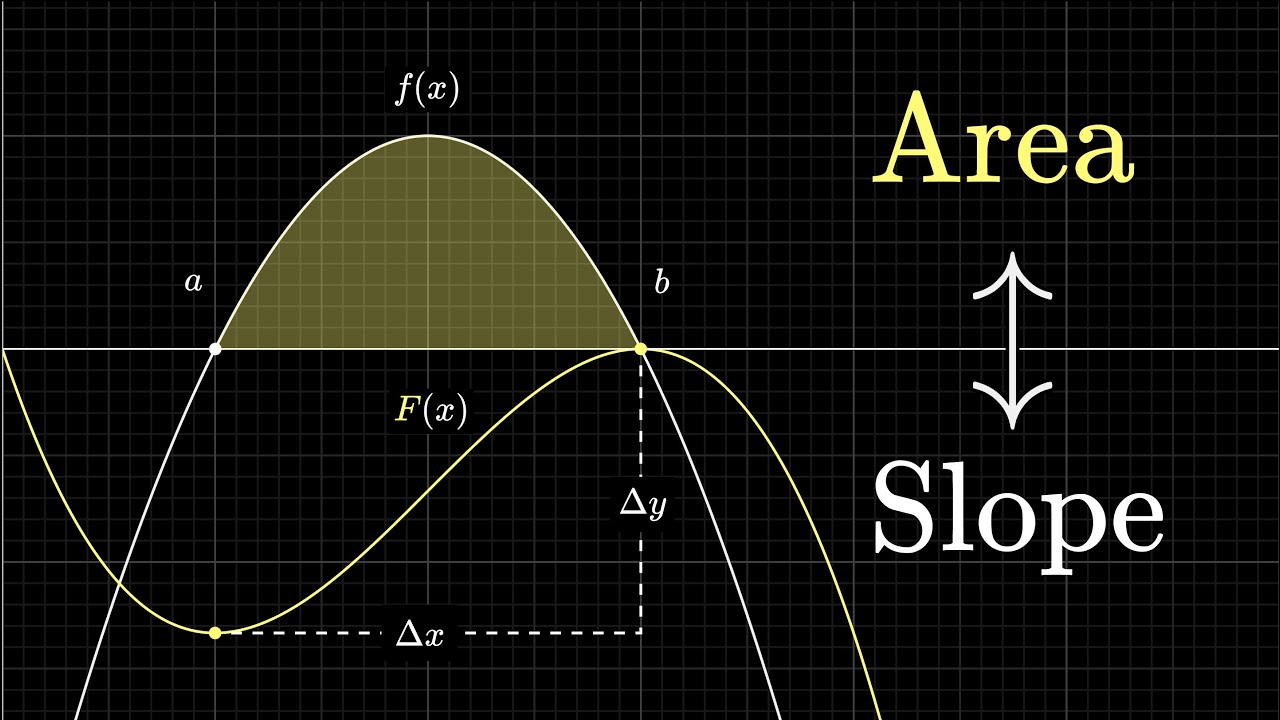([View Highlight](https://read.readwise.io/read/01jfmq1pttssfvb5dhw13q6vmz)) --- this average will approach the actual integral of $\sin(x)$ between 0 and $\pi$, all divided by the length of that interval, $\pi$. In other words, the average height of this graph is this area divided by its width. On an intuitive level, and just thinking in terms of units, that feels pretty reasonable, doesn't it? Area divided by width gives you an average height. ([View Highlight](https://read.readwise.io/read/01jfmq32sgbpwxe52ctmvafm6e)) ^q1atex - Tags: [[👻 ai highlighted]] --- Notice how finding this average value, $\frac{2}{\pi}$, came down to looking at the change in the antiderivative, $-\cos(x)$, over the input range, divided by the length of that range. And another way to think about that fraction is as the rise over run slope between the point of the antiderivative graph below 0 and the point of that graph above $\pi$. Think about why it might make sense that this slope would represent an average value of $\sin(x)$ on that region. By definition, $\sin(x)$ is the derivative of this antiderivative graph, giving us the slope of $-\cos$ at every point. Another way to think about the average value of $\sin(x)$ is as the average slope over all tangent lines between 0 and $\pi$. And when you view things like that, doesn't it make a lot of sense that the average slope of a graph over all its points in a certain range should equal the total slope between the start and end points? ([View Highlight](https://read.readwise.io/read/01jfmq66bseab92ax4tdpjbe9s)) - Tags: [[👻 ai highlighted]] ---